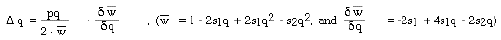(or we can calculate w of each genotype).Selection, Mutation, Drift, and Gene Flow
Interactions between Selection, Mutation, Drift, and Gene Flow
How efficient is natural selection at eliminating unfavorable mutations?
How rapidly will a favorable mutation spread through a population?
This lecture is an introduction to the four forces of genetic apocalypse:
1) selection, 2) mutation, 3) genetic drift, and 4) population gene flow.
Hardy-Weinberg maintains gene frequencies at an equilibrium in the absence
of other forces. The four parameters change gene frequencies and typically
perturb Hardy-Weinberg equilibrium. Studying parameters in tandem (push
me pull you style) will develop a picture of evolutionary equilibrium between
forces.
Components of this lecture are available as a simulation exercise. VERY IMPORTANT: Before running the simulation for each excercise, draw a graph of what you expect to happen (these graphs must be made for you to understand the simulations, trust me).
The equations used to simulate selection can be readily derived in using
algebra very similar to that used for the H-W equilibrium. Change in gene
frequency under the force of selection is given by:
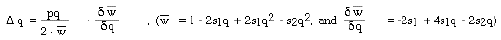(or we can calculate w of each genotype).
wbar is average fitness. d(wbar)/dq is how the derivative of wbar as
a function of gene frequency or how rapidly fitness goes up or down with
a unit change in gene frequency. p*q is 1/2 the frequency of heterozygotes.
Heterozygotes are a large reservoir of genetic variability.
Exercise: Let us first simulate a simple case of overdominance (the heterozygote is the most fit genotype). Before you begin, draw a graph of what you expect to see for gene frequency versus time (generations). To see how selection works in the simulation let us set N=1000, p=0.1 (initial frequency of A), wAA=0.9, wAa = 1.0, and waa=0.9 (We should have both u=0, NGen=100, Npops = 8, isolated populations). What happens? Why? Now set Waa=1.0 (all else remains the same). In this case we have allele "A" recessive to "a" in fitness (or "a" is dominant, genotype "aa" has the highest fitness and its fitness is the same as "Aa", remember A does not always have to be dominant!!!!). Play with strength of selection. How rapidly does the gene frequency become fixed? How do the simulated curves compare to your earlier "intuitive" graph. Why is the trajectory of gene frequency S-shaped? That is why does change in gene frequency slow down when the allele is close to fixation shouldn't it be linear???
Overdominance occurs when the heterozygote at a locus has a higher fitness than either homozygote.
One the best known examples of overdominance is sickle cell hemoglobin in humans.
The HbA allele is the normal allele, HbS is the sickle cell allele.
Individuals who are homozygous for the HbA allele are susceptible to malaria in West-central Africa.
Homozygotes for the HbS allele suffer from a severe anemia.
HbA | HbS heterozygotes enjoy resistance to malaria but do not suffer from anemia.
The fitness of the three genotypes is: AS > AA > SS.
The polymorphism persists despite the suffering of AA and SS homozygotes.
How can we explain the high frequencies of many deleterious mutations.
Cystic fibrosis, tay sachs, and a number of other genetic maladys can occur
at a very high frequency in a population
In natural populations, mutation typically occurs at very low rates,
values from 10-3 - 10-4 per gene per generation are fairly typical. The
equilibrium gene frequency for q as derived in lecture is given by:
mA->a | |
| qequil = | __________ |
| mA->a + mA->a |
(where mA->a & mA->a are the forward mutation rates: A -> a, and backward mutation rates a -> A respectively).
Exercise: Things happen really slowly if we were to use realistic
mutation rates. So, let's say we have outrageously high mutation rates (mA->a
= 10-1 = 0.1 and ma->A = 10-2 = 0.01),
p=0.0 (i.e., there are no A alleles around). Unfortunately, the population
of field mice you were studying was in Love Canal or really close to Three
Mile Island. Set wAA=wAa=waa=1 (the mutations are not deleterious in any
way, they are neutral). Notice that the populations come to an equilibrium
that is given by the above formula (use a calculator to verify). Now lets
start decreasing both mutation rates by an order of magnitude. It just takes
longer to reach equilibrium. By itself, mutation is a very weak force. Especially
if we consider it relative to selection in which s1, s2 = 1 to 10-2 to very
small values (e.g., 10-4 which would be comparable to mutation rates).
Did you notice how all the simulation lines are wiggly? Even for a relatively
large population N=1000, the gene frequencies will drift. The critical concept
with genetic drift is effective population size usually termed Ne. Ne is
the number of adults that contribute to the "gene pool" each generation.
Many factors can alter (always reduce) Ne relative to N the actual number
of individuals in a population. For example differences in mate success
(some males get more copulation's) lowers Ne. This alteration in effective
sex ratio has the following effect on Ne relative to observed number of
males and females:
| Nm*Nf | |
| Ne = | ______ |
| Nm+Nf |
Verify for yourself that Ne=N when the sex ratio is equal to 1. Then,
calculate Ne for a population of 25 males and 100 females (N=125). Two of
the many other factors that reduce Ne include natural selection and non-overlapping
generations (offspring perhaps mate with parents, etc.).
Exercise: Change the relative fitness of all three genotypes to 1 (no selection, set both mutation rates to 0, set the initial freq. p = 0.5. Start out with Ne = 1000. Let us decrease Ne by 1/2 on each simulation cycle (e.g., Ne = 500 on the next cycle, and so on ...125, 64, 32, 16). What happens? Is genetic drift a creative force like mutation, or is it a destructive force like selection (i.e.., does it create variation or reduce it)? What inevitably happens to gene frequencies in small populations?
Random genetic drift can be very prevalent when populations experience "genetic bottlenecks" or "founder effects". A genetic bottleneck is defined as an extreme reduction in population size that persists over a number of generations which the population eventually recovers. During this period of reduced size, the loss of variation due to random drift will be pronounced. Two of the most extreme examples of known or suspected bottlenecks involve the northern elephant seal (Mirounga angustirostis) and the cheetah (Acinonyx jubatus).
Populations of the East-African and South African subspecies of the cheetah have been surveyed for 52 loci. A sample of 30 individuals from the EAP gave P = 0.04 and H = 0.01. From a sample of 98 individuals from the South African group, P = 0.02, and H = 0.004.
These are extremely low estimates. Even more surprising was the finding that skin grafts among unrelated individuals from the South African subspecies are not rejected. This suggests that the cheetah is monomorphic at its major incompatibility or MHC locus which is abundantly polymorphic in all other mammals.
Further evidence that the cheetah is possesses diminished levels of variation comes from observations that male cheetahs have a high incidence of abnormal spermatozoa and attempts to mate cheetahs in captivity have met with little success.
Furthermore, a recent outbreak of feline infectious peritonitis in the 1980's severely decimated many colonies of animals. It is interesting that the same virus caused only a 1% mortality rate in domestic cats. These observations support the suggestion that cheetahs have lost much of their reservoir of genetic variability and thus may be precariously poised on the brink of extinction.
Unlike the elephant seal there is no direct evidence for a bottleneck
in the species' recent history. However, it is known that the cheetah used
to have a much larger geographic range. Athough it is now endemic to the
African subcontinent, it used to be found throughout Europe and Asia. Apparently,
the species has undergone at least two severe bottlenecks resulting in the
loss of much of their genetic variation.
The mixing of gene pools from isolated populations with different gene frequencies tends to reduce heterozygosity (Wahlund effect). (e.g., adults oysters are found in estuaries however, their gametes and offspring disperse out of the estuary and contribute to the total population of oysters [all estuaries]). There are several models of gene flow including:
a) continent-island or source-sink: one-way gene flow from a continent which has a large population to a smaller "island" population;
b) island model in which migration occurs among islands (usually all islands have equal probabilities of receiving dispersing individuals and thus the migration rate or gene flow is considered to be equally distributed among all islands);
c) stepping stone model in which each island is more likely to receive migrants from adjacent islands than from islands farther away. The stepping stone model in this program is one in which islands form a ring, and each island receives migrants from adjacent islands only.
Migration homogenizes gene frequencies among populations. We can't simulate
the process of homogenization with this program because we can't start out
with different gene frequencies in our replicate populations. However, as
you will see later, genetic drift erodes variation (loose alleles from the
population). Gene flow tends to limit erosion that is caused by genetic
drift because it homogenizes the populations that are drifting apart in
gene frequency. The effect of gene flow is most interesting when it is considered
in combination with other forces:
Exercise: Let's simulate the process of local adaptation. Assume
that the allele "a" is very beneficial on an island such that
wAA=0.8, wAa = 0.8, and waa=1 (allele a is a beneficial recessive allele
on the island). However, on the mainland, the genotype frequency is
fixed for all AA (Only AA survive there: that means that you set the value
for p=1.0 on the mainland, top right slider). Migration from the mainland
to each island is a modest m = 0.1 (remember to set both u=0, Ne=1000, NGen=100,
Npops = 8). Start with 8 isolated populations. Change it to source-sink
model. What happens to gene frequency?
There are two interesting cases that reveal how mutation is an important force in evolution. Both cases involve selection. The first case involves mutation-selection balance in which deleterious recessives are under chronic selection. The rate at which deleterious mutations arise (forward mutation) is always generally higher than the rate at which they might mutate back to a functional gene. Presumably, chronic selection should eliminate such alleles. In this sense selection is purifying in that it tends to eliminate deleterious mutations.
Exercise: Run the simulation program with: N=1000, p=0.5 (initial
frequency of A), wAA=1.0, wAa = 1.0, and waa=0.5 (We should have ua->A
= 10-3, NGen=100, Ne=1000, Npops = 8, isolated populations). Why isn't the
"a" allele eliminated from the population? Test the hypothesis
that it is mutation that prevents rapid fixation of the "a" allele
-- set the mutation rate to zero. Does allele then disappear from the population
rapidly? This is an important concept and is directly related to questions
asked at the end of section 1) on selection. Incidentally, the equilibrium
gene frequency for mutation selection balance of a deleterious recessive
allele is given by:
qequil =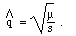 
How does this formula compare with the simulation?
A partial answer to the above question (why isn't allele "a" eliminated?) is given by changing wAa = 0.9. This makes allele a partially dominant. The equilibrium gene frequency for a partially dominant allele is given by:
qequil = m/(s*h)
where s is given by the selection against aa genotype (e.g., relative
fitness of aa is 1-s1 relative to 1 for the AA genotype), and h is given
by (1-h) which corresponds to our 1-s2 (or the degree
of dominance in fitness). This reflects the fact that possession of
one copy of allele "a" has a small effect on fitness of Aa genotype
and is thus partially dominant. What is the difference between a
deleterious recessive (complete recessive) and a partially dominant one
in terms of evolutionary dynamics? Play around with the degree of dominance.
Again, test the hypothesis that it was mutation that prevents rapid fixation
of the "a" allele -- set the mutation rate to zero. Does allele
"a" disappear from the population rapidly when it has an effect
in both homozygotes and heterozygotes? Compare this result with the test
for mutation above.
The second relevant case of mutation-selection deals with the spread of novel beneficial alleles in populations. Just how long does it take for an allele to sweep through a population?
Exercise: Run the simulation starting with the following parameters wAA=0.5, wAa = 0.5, and waa=1.0 (allele "A" is the wild type allele relative to the mutation "a" that has twice the fitness). Set p = 1.0 (remember to set ua->A = 0 and uA->a = 0.0001 (or 10-4), NGen=1000, Npops = 8, isolated populations). We can only realistically simulate a population size of Ne=1000, not an infinite population. For this population allele "a" will only arise every 10 generations on average (why is this so?). Why does it take so long for "a" to make it into the population (hint: it has something to do with another evolutionary parameter as well as the effects discussed at the end of Section 1) ) despite it being so beneficial? It also has to do with the following simulation results. What happens if we change wAa = 0.6 (allele a now has partially dominant effect on fitness)?
The WHO estimates that 23 million people were infected with the HIV virus in 1996.
The HIV virus is a retrovirus (RNA virus) responsible for indirectly producing a disease known as AIDS.
Briefly, the virus accomplishes this by infecting a key player in the vertebrate immune system called helper T cells.
By infecting helper T cells, our body's own immune system responds and ends up destroying our T cell population over time.
A lot of excitement was generated about 10 years ago by an AIDS drug called AZT (azidothymidine).
Coupled with the high mutation rate, we can estimate that the HIV virus can evolve over a ten year period to the same extent that humans can over a period of a million years!
Conclusion: no single drug can halt HIV infection - multiple drugs
can, though.
Part of the answer to the last set of questions involved drift. Even
for a relatively large population (N = 1000), drift may keep allele "a"
at a very low frequency despite fairly strong selection favoring allele
"a".
Exercise: Let us see how Ne effects the probability of fixation
of a beneficial allele. Run the simulation starting with the following parameters
wAA=1.0, wAa = 0.9, and waa=0.9. The initial frequency of pA = 0.3 (remember
to set uA->a = 0 and ua->A = 0, NGen=1000, Ne=1000, Npops = 8, isolated
populations). How fast does allele "A" fix in the population?
What happens if we start decreasing Ne? Reduce Ne to 400, 80, and 40. With
Ne set to 40, run the simulation several times (get at least 8 populations
X 10 replicate runs? How many times does allele "A" get fixed?
How many times does allele "a" get fixed?. What does this tell
you about the likelihood of a moderately beneficial allele becoming fixed?
What happens if we change the degree of dominance.
| Occurs where? | Magnitude determined by | Relative Effect in a small population | Relative Effect in a large population | |
| Selection | within | w | very strong | very strong |
| Mutation | within | u | weak | weak |
| Random Drift | within | Ne | moderate | weak |
| Gene Flow | among | m | strong | strong |